[最も共有された！ √] 空間 図形 体積 266956

数学 大学入試良問集 19 23 空間図形の断面積と体積 を宇宙一わかりやすく Youtube

平面・空間図形 128 球の体積・表面積公式の覚え方は語呂合わせで！ 円柱の計算体積、表面積の求め方はこれでバッチリ！ 平面・空間図形 113第6章 空間図形 ＜＜ L44 球の表面積と体積 の問題に戻る L45 切り取った立体の体積 の解答表示 ＞＞ 練習問題1 右図の12は、立方体をある平面で切り取って、その切り口に色をつけたものです。 このとき、以下の問いに答えなさい。 1 2点B，Dと

空間 図形 体積

空間 図形 体積-G04～07 空間図形 体積・表面積 (1) (2) 中心角 (3) 1 右の図のように、底面の半径が3cm、母線の長さ5cm、高さが4cmの円錐がある。 これについて、次の問いに答えなさい。 この円錐の体積を求めよ。 この円錐の側面はおうぎ形である。 の大きさを求めよ。空間図形 立方体を切断したときの切り口の考え方 空間図形 角柱・角錐(すい)・円柱・円錐の体積の求め方 空間図形 円柱の側面積の求め方がわかりません。 空間図形 母線とは何か 空間図形 「辺に垂直な面がどこか」という問題

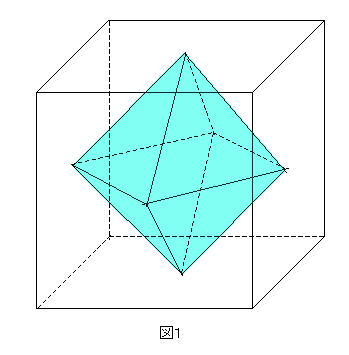
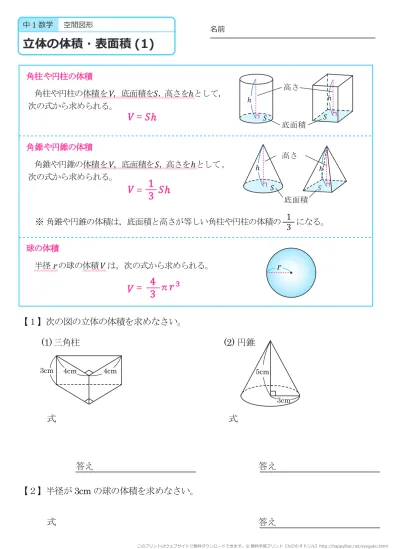
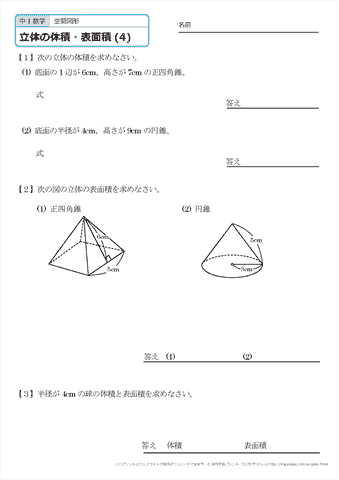
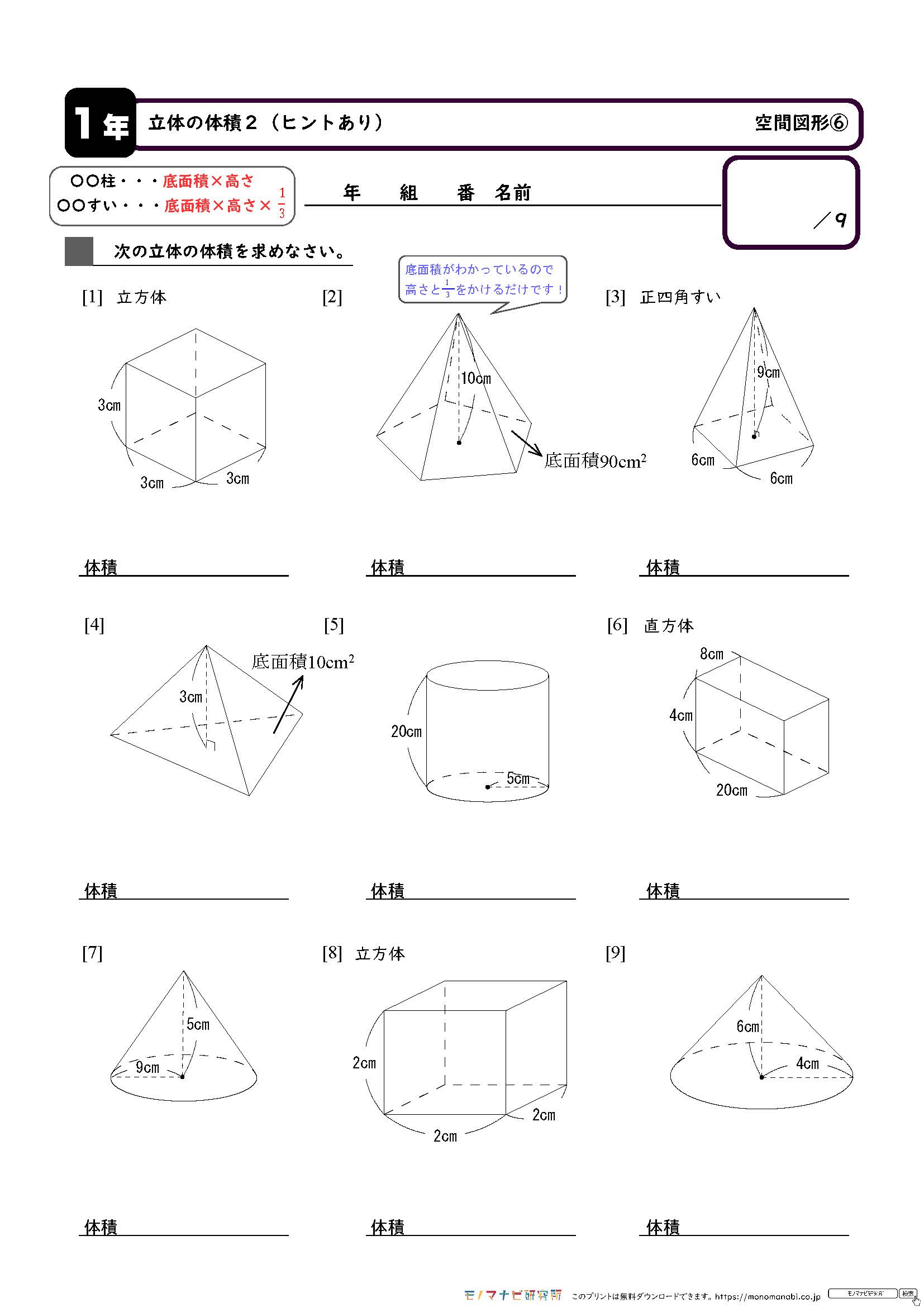
無料 中１数学 基本問題 問題プリント 空間図形６ 立体の体積 143

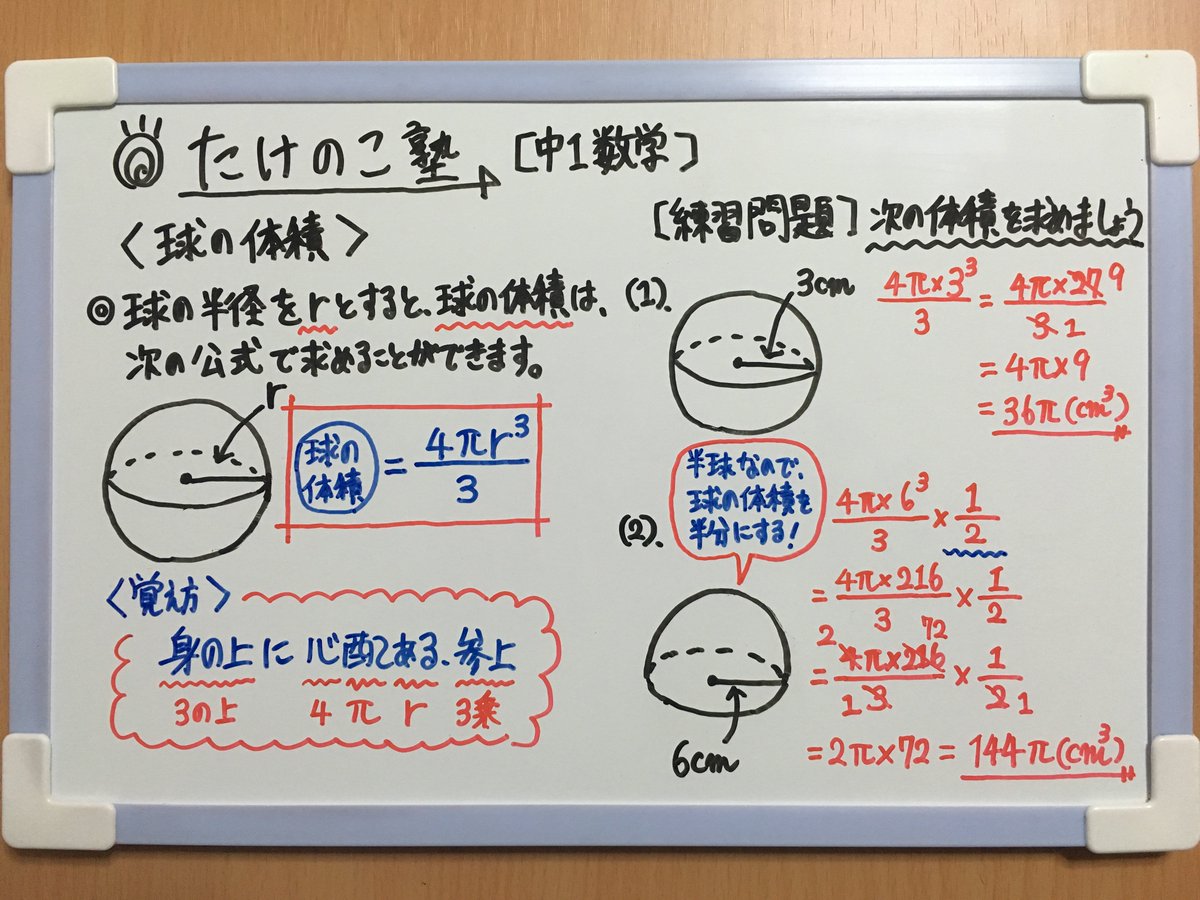
 球の体積の求め方の公式が覚えられねえ！！ こんにちは！この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、2章 空間図形 48 140 次の図の立体の体積を求めよ。 ⑴ ⑵ 138 次の図の角錐の体積を 求 めよ 。 ⑴ ⑵ ⑶ 141 右の図のよ う に ，1 辺 12 cm の立方体から，3 点 A ，C ，F を通る平 面で切ってできる 2 つの立体のうち，小さい方の立体を取り除いた。空間図形(発展) 解説 1 図は一辺12㎝の立方体である。 ap=3㎝、bq=7㎝とする。 d,p,qを通る平面でこの立方体を切ったときの切り口をdpqsとする。

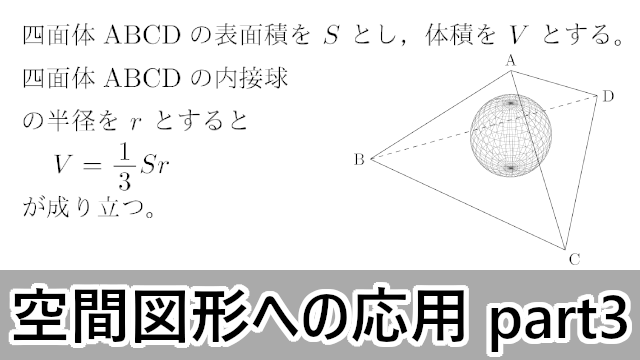
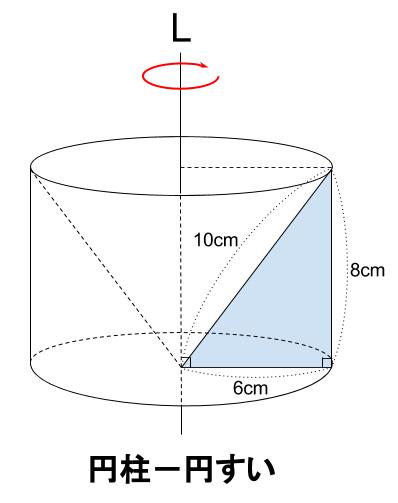
 中1数学「空間図形」の3回目です。 今回は体積の問題で中学生がつまずきやすいところを解説します。 柱・錐・球それぞれ、入試問題中心に計6例題。 ぜんぶ応用問題ですので、基本を学んだうえで「でも、じっさいのテストになるとできない」って生徒にご参考ください。空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底 次の図形を直線を軸として1回転してできる回転体の体積、表面積を求めなさい。 正方形、長方形を回転させると円柱ができます。 つまり、上の図のような円柱の体積、表面積を求めれば良いということになります。 体積 体積は、 底面積 高さ を

空間 図形 体積のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「空間 図形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。

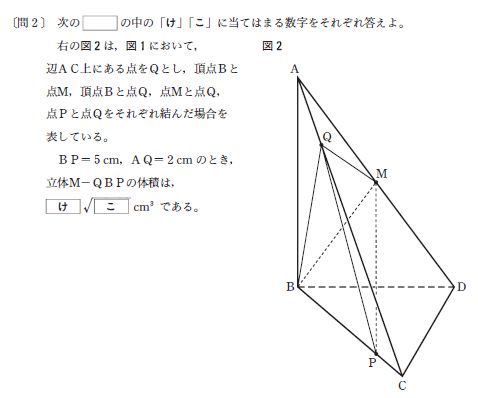
空間図形 問題 角柱、角すい 直線と直線の位置関係 直線と平面の位置関係 平面と平面の位置関係 平面が動いてできる立体 立体の展開図 おうぎ形の弧の長さ おうぎ形の中心角 おうぎ形の利用 体積 応用問題空間図形 (発展) 図は一辺12㎝の立方体である。 AP=3㎝、BQ=7㎝とする。 D,P,Qを通る平面でこの立方体を切ったときの切り口をDPQSとする。 (1) CS の長さを求めよ。 (2) 切断してできる立体のうち頂点Bを含むほうの立体の体積を求めよ。 図のような1辺6cmの立方